
3분만 투자하세요! 분자 궤도 함수의 신비로운 세계를 탐험하고, 화학 결합의 원리를 꿰뚫어 보는 즐거움을 누려보세요. 복잡한 화학 용어는 잊어버리고, 쉽고 명확한 설명으로 분자 궤도 함수의 개념을 완벽하게 이해하게 될 거예요. 준비되셨나요? ✨
분자 궤도 함수란 무엇일까요?
분자 궤도 함수(Molecular Orbital, MO)는 원자 궤도 함수들이 결합하여 만들어지는 함수를 말해요. 마치 레고 블록처럼 여러 개의 원자 궤도 함수가 서로 결합하여 새로운 형태의 궤도 함수, 즉 분자 궤도 함수를 형성하는 거죠. 각 원자는 자체의 원자 궤도 함수를 가지고 있고, 이들이 서로 가까워지면 상호작용하여 분자 궤도 함수를 만들게 됩니다. 이 과정에서 전자들은 새로운 에너지 준위를 가지는 분자 궤도 함수에 들어가게 되고, 이것이 바로 화학 결합의 핵심이랍니다. 쉽게 말해, 분자 궤도 함수는 분자 내에서 전자들이 존재할 수 있는 공간을 나타내는 함수라고 생각하면 돼요. 이 함수의 모양과 에너지는 분자의 성질, 특히 결합의 강도와 성격을 결정하는데 중요한 역할을 한답니다. 😊
분자 궤도 함수의 종류는 무엇일까요?
분자 궤도 함수는 크게 결합성 분자 궤도 함수와 반결합성 분자 궤도 함수로 나뉘어요. 결합성 분자 궤도 함수는 원자 궤도 함수들이 서로 보강 간섭을 일으켜 전자의 밀도가 원자핵 사이에 집중되는 궤도 함수를 말하는데요. 이는 결합을 강화시키는 역할을 합니다. 반면, 반결합성 분자 궤도 함수는 원자 궤도 함수들이 상쇄 간섭을 일으켜 전자의 밀도가 원자핵 사이에서 낮아지는 궤도 함수에요. 이는 결합을 약화시키는 역할을 하죠. 두 궤도 함수의 에너지 준위는 다르며, 결합성 궤도 함수의 에너지 준위가 더 낮아요. 전자들은 항상 낮은 에너지 준위를 선호하기 때문에, 결합성 분자 궤도 함수가 먼저 채워집니다. 그리고 이러한 결합성과 반결합성 궤도의 에너지 차이가 결합의 세기를 결정하는 중요한 요소가 된답니다. 흥미롭죠? 🤔
분자 궤도 함수와 결합 차수는 어떻게 관련될까요?
결합 차수는 분자 내에서 결합에 기여하는 전자의 수를 나타내는 지표인데요. 결합 차수는 (결합성 전자 수 – 반결합성 전자 수) / 2 의 공식으로 계산할 수 있어요. 결합 차수가 클수록 결합이 강하고, 분자는 더 안정적이에요. 예를 들어, 산소 분자(O₂)의 경우, 결합성 궤도 함수에 8개의 전자가, 반결합성 궤도 함수에 4개의 전자가 존재하므로, 결합 차수는 (8-4)/2 = 2가 되죠. 이것은 이중 결합을 의미하며, 산소 분자의 강한 결합을 설명해 줍니다. 결합 차수는 분자의 안정성과 반응성을 이해하는 데 매우 중요한 개념이랍니다. 이제 결합 차수를 계산하는 방법을 이해하셨나요? 👍
분자 궤도 함수 다이어그램 해석하기
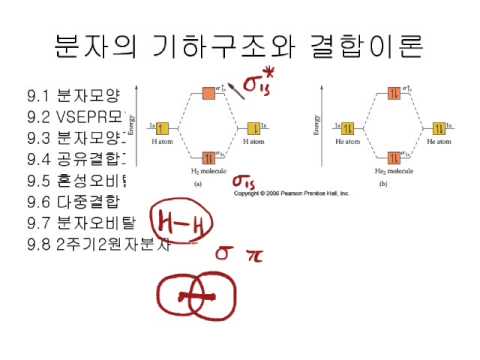
분자 궤도 함수 다이어그램은 원자 궤도 함수가 결합하여 분자 궤도 함수를 형성하는 과정을 시각적으로 보여주는 도구에요. 다이어그램을 해석하면, 분자의 결합 차수, 자기적 성질, 그리고 분자의 에너지 준위 등을 알 수 있어요. 다이어그램은 에너지 준위에 따라 분자 궤도 함수들을 배열하고, 각 궤도 함수에 전자들이 채워지는 모습을 보여줍니다. 각 원자의 원자 궤도 함수들이 어떻게 결합하여 분자 궤도 함수를 형성하는지, 그리고 전자들이 어떤 궤도 함수에 채워지는지를 이해하는 것이 중요해요. 이를 통해 분자의 특성을 예측하고 이해할 수 있답니다. 다이어그램을 보는 연습을 충분히 하면, 분자의 성질을 한눈에 파악할 수 있을 거예요! 🤓
다원자 분자의 분자 궤도 함수는 어떻게 다를까요?
두 원자로 이루어진 이원자 분자와 달리, 세 개 이상의 원자로 이루어진 다원자 분자의 분자 궤도 함수는 훨씬 복잡해요. 이러한 복잡성은 여러 개의 원자 궤도 함수들이 상호작용하기 때문인데요. 다원자 분자의 분자 궤도 함수를 계산하고 해석하는 것은 상당히 어려운 작업이지만, 근사적인 방법들을 사용하여 분자의 성질을 예측할 수 있어요. 예를 들어, Hückel 근사법과 같은 방법들을 사용하면 다원자 분자의 분자 궤도 함수를 계산하고 해석하는 데 도움을 받을 수 있죠. 이러한 방법들은 다원자 분자의 전자 구조를 이해하는 데 중요한 역할을 한답니다. 복잡해 보이지만, 기본 원리를 이해하면 다원자 분자의 분자 궤도 함수도 이해할 수 있을 거예요! 💪
분자 궤도 함수 이론의 응용은 무엇일까요?
분자 궤도 함수 이론은 단순한 이론적인 개념을 넘어 다양한 분야에서 실제로 응용되고 있어요. 재료 과학에서는 새로운 재료의 설계 및 합성에 활용되고 있고, 화학 반응의 메커니즘을 이해하고 예측하는 데에도 중요한 역할을 하고 있습니다. 특히 촉매 작용의 원리를 이해하고 효율적인 촉매를 개발하는 데 필수적인 이론이기도 합니다. 또한, 분자의 스펙트럼을 해석하고 분자의 구조를 밝히는 데에도 사용되며, 생화학 분야에서는 생체 분자의 구조와 기능을 이해하는 데 활용되고 있어요. 분자 궤도 함수 이론의 응용 범위는 매우 넓고, 앞으로도 더욱 다양한 분야에서 활용될 것으로 기대됩니다. 흥미로운 사실이죠? 💡
“분자 궤도 함수” 핵심 내용 요약

- 원자 궤도 함수의 결합으로 생성된 함수입니다.
- 결합성 및 반결합성 궤도로 나뉘며, 결합 차수를 결정합니다.
- 다이어그램 해석을 통해 분자의 특성을 예측할 수 있습니다.
분자 궤도 함수 후기 및 사례
저는 개인적으로 분자 궤도 함수 이론을 배우면서 화학 결합의 본질을 더욱 깊이 이해하게 되었어요. 처음에는 복잡하게 느껴졌지만, 꾸준히 공부하고 다이어그램을 그려보면서 점점 더 명확하게 이해할 수 있었답니다. 특히, 다양한 분자의 분자 궤도 함수 다이어그램을 직접 그려보는 연습은 매우 유익했어요. 이를 통해 각 분자의 결합 차수와 자기적 성질을 직접 확인하고 예측할 수 있었죠. 또한, 이론을 통해 예측한 결과를 실제 실험 결과와 비교해보면서 이론의 정확성과 한계를 경험할 수 있었던 것도 좋은 경험이었습니다. 분자 궤도 함수 이론은 화학을 이해하는 데 있어서 매우 중요한 기초이므로, 꾸준히 공부하는 것을 추천드립니다. 😄
자주 묻는 질문 (FAQ)
Q1: 분자 궤도 함수 이론은 어떤 원리에 기반한 것인가요?
A1: 분자 궤도 함수 이론은 양자역학의 원리에 기반한 이론으로, 원자 궤도 함수들이 서로 상호작용하여 분자 궤도 함수를 형성한다는 개념을 설명합니다. 이러한 상호작용은 전자들의 파동 함수의 중첩으로 이해될 수 있으며, 보강 간섭과 상쇄 간섭에 따라 결합성 및 반결합성 분자 궤도 함수가 생성됩니다.
Q2: 분자 궤도 함수 다이어그램을 해석하는 방법은 무엇인가요?
A2: 분자 궤도 함수 다이어그램은 에너지 준위에 따라 분자 궤도 함수를 배열하고, 각 궤도 함수에 전자들이 채워지는 모습을 보여줍니다. 다이어그램을 해석할 때는, 결합성 궤도와 반결합성 궤도의 개수를 세어 결합 차수를 계산하고, 전자의 배열을 통해 분자의 자기적 성질 (이온성, 공유성 등)을 확인해야 합니다.
Q3: 분자 궤도 함수 이론의 한계는 무엇인가요?
A3: 분자 궤도 함수 이론은 복잡한 분자에 대해서는 정확한 계산이 어렵다는 한계를 가지고 있습니다. 특히 다원자 분자의 경우, 근사적인 방법을 사용해야 하며, 이러한 근사는 계산의 정확도를 떨어뜨릴 수 있습니다. 또한, 전자 상관 효과를 완벽하게 고려하지 못하는 경우도 있습니다.
함께 보면 좋은 정보: 분자 궤도 함수 관련 심화 내용
1. 혼성 궤도 함수 (Hybrid Orbitals)
혼성 궤도 함수는 서로 다른 원자 궤도 함수들이 섞여 새로운 궤도 함수를 형성하는 것을 말해요. 예를 들어, 탄소 원자의 경우, s 궤도 함수와 p 궤도 함수가 섞여 sp, sp², sp³ 혼성 궤도 함수를 형성합니다. 이러한 혼성 궤도 함수는 분자의 구조와 결합 각도를 설명하는 데 매우 중요한 역할을 하죠. 혼성 궤도 함수의 개념을 이해하면, 다양한 분자의 구조와 결합 특성을 더욱 깊이 이해할 수 있을 거예요. 혼성 궤도 함수는 분자의 구조를 결정하는 데 중요한 역할을 하므로, 분자 궤도 함수와 함께 이해하는 것이 중요합니다.
2. 분자 궤도 함수 계산 방법 (Computational Chemistry)
분자 궤도 함수는 이론적으로 계산할 수 있어요. 양자 화학 계산을 통해 분자의 전자 구조와 분자 궤도 함수를 얻을 수 있습니다. 여러 가지 계산 방법이 있지만, 가장 널리 사용되는 방법 중 하나는 Hartree-Fock 방법입니다. 이 방법은 전자 상관 효과를 고려하지 않지만, 비교적 간단하고 빠르게 계산할 수 있어서, 많은 분자 시스템에 적용될 수 있습니다. 더욱 정확한 계산을 위해서는, 후쿠다 방정식, 밀도 범함수 이론 (Density Functional Theory, DFT) 등이 사용됩니다. 이러한 계산 방법들은 실험적으로 얻기 어려운 분자의 정보를 얻는 데 중요한 역할을 한답니다.
3. 분자 궤도 함수와 분광학 (Spectroscopy)
분자 궤도 함수의 에너지 준위 차이는 분광학적 분석을 통해 관찰될 수 있어요. 자외선-가시광선 분광법 (UV-Vis Spectroscopy), 적외선 분광법 (IR Spectroscopy), 자기 공명 분광법 (NMR Spectroscopy) 등을 이용하여 분자의 전자 전이, 진동, 회전 등에 대한 정보를 얻을 수 있습니다. 이러한 분광학적 정보를 분석하여 분자의 구조와 성질에 대한 정보를 얻을 수 있고, 이 정보는 분자 궤도 함수 이론을 검증하고 발전시키는 데 중요한 역할을 합니다. 즉, 분광학은 분자 궤도 함수 이론을 실험적으로 확인하는 중요한 도구라고 할 수 있어요.
‘분자 궤도 함수’ 글을 마치며…

이 글을 통해 분자 궤도 함수에 대한 이해가 조금 더 깊어졌기를 바랍니다. 처음에는 어렵게 느껴질 수 있지만, 차근차근 개념을 이해하고 다이어그램을 그려보면서 익숙해질 수 있을 거예요. 분자 궤도 함수 이론은 화학의 기본 원리를 이해하는 데 매우 중요한 역할을 하며, 다양한 분야에 응용될 수 있는 강력한 도구입니다. 이 글이 여러분의 화학 공부에 조금이나마 도움이 되었으면 좋겠고, 앞으로도 화학의 흥미로운 세계를 탐험하는 데 즐거움을 느끼시기를 바랍니다! 💖
분자 궤도 함수 관련 동영상

분자 궤도 함수 관련 상품검색






